(hpd/rdf) “Spurious correlations” ist die neue Lieblingswebsite eines jeden Skeptikers. Die Website ist brillant: Sie gräbt in den unterschiedlichsten Datensätzen (etwa zu den Themen Todesursachen, Verzehr diverser Produkte, Scheidungsraten der einzelnen Staaten usw.) und versucht dann, Korrelationen zwischen den verschiedenen Variablen zu finden. Die Resultate sind oft äußerst unterhaltsam.
Der Sinn dieser Übung besteht darin aufzuzeigen, dass Korrelation nicht unbedingt Kausalität bedeuten muss. Es ist oft effektiver, ein Prinzip zu veranschaulichen, als es zu erklären. Indem man beeindruckende grafische Korrelationen zwischen Phänomenen bietet, die offensichtlich nicht miteinander in ursächlicher Verbindung stehen (oder eine solche zumindest oberflächlich betrachtet absurd erscheint), bringt man die Tatsache auf den Punkt, dass Korrelation alleine nicht auf Kausalität schließen lässt.
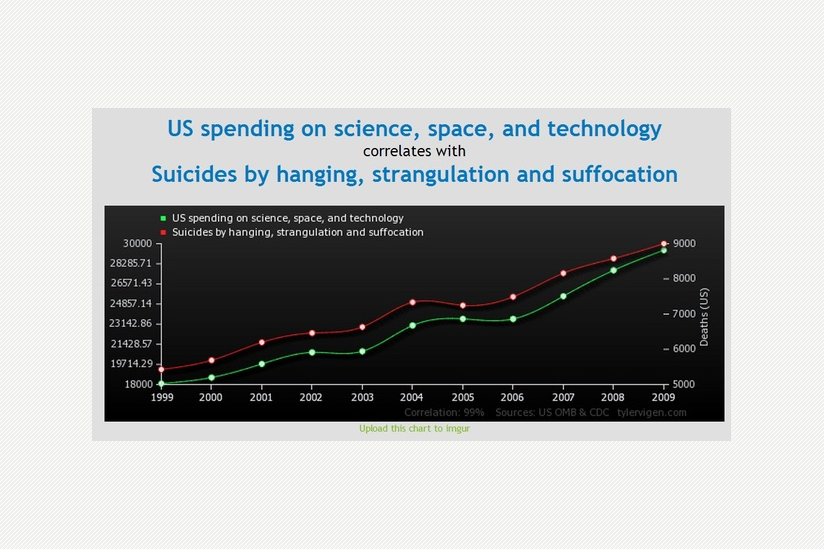
Ich glaube, die meisten Menschen verstehen intuitiv, dass es unwahrscheinlich ist, dass die Finanzierung von Raumfahrt, Wissenschaft und Technologie mit Selbstmorden durch Erhängen, Strangulation oder Ersticken in irgendeinem sinnvollen ursächlichen Zusammenhang steht.
Und doch – sehen Sie sich den Kurvenverlauf an. Wenn ein ähnliches Diagramm zwei Variablen zeigte, die möglicherweise in Kausalzusammenhang stehen, würde es sehr überzeugend wirken.
Auf ein paar Überlegungen zu diesem Thema möchte ich näher eingehen. Zunächst wäre da der wichtige Vorbehalt, dass die Korrelation zwar nicht notwendigerweise Kausalität bedeutet, aber mitunter eben doch. Zwei Variablen, die miteinander in ursächlichem Zusammenhang stehen, korrelieren auch miteinander. Die mitunter gebotene übermäßige Vereinfachung: „Korrelation bedeutet nicht Kausalität“ lehne ich ab. Denn manchmal ist es so.
Der zweite Punkt ist ein statistischer. Die wichtige, tiefere Lektion hier betrifft die Macht des “Data-mining” [gezielte Datensuche und –auswertung zur Erkennung neuer Muster, Gesetzmäßigkeiten und verborgener Zusammenhänge, Anm. d. Übers.]. Menschen fällt es leicht, große Datenmengen zu durchsieben und scheinbare Muster darin zu entdecken. Tatsächlich verfügen wir in dieser Hinsicht über eine starke, einseitige Neigung, “falsch positive Resultate” zu finden - wir finden Muster, die nicht wirklich da sind, sondern die auf statistische Zufallstreffer oder schlichtweg auf falsche Vorstellungen zurückzuführen sind.
Doch Korrelationen kommen uns überzeugend vor. Wenn man von einem Freund träumt, den man seit 20 Jahren nicht mehr gesehen hat, und am nächsten Tag ruft er an, dann erscheint einem diese Korrelation unheimlich, und man sucht nach einer Ursache. Wir sind uns nicht einmal der Tatsache bewusst, dass wir aufgrund dieser anscheinend verblüffenden Korrelation riesige Datenmengen durchforsten – nämlich alles, was uns den ganzen Tag lang widerfährt. Die Möglichkeiten zufälliger Korrelationen sind enorm, und es ist nicht überraschend, wenn wir manche finden. Die erwähnte Website macht im Prinzip dasselbe, nur mit grafischen Daten. Sie durchsiebt große Mengen an Grafiken und findet falsche Korrelationen.
Dies geschieht manchmal auch mit veröffentlichten Daten, auch wenn es nicht ganz offensichtlich ist. Wissenschaftler arbeiten sich mitunter durch viele Daten auf der Suche nach möglichen Korrelationen, bis sie auf eine stoßen. Vielleicht veröffentlichen sie all die möglichen Korrelationen, nach denen sie gesucht haben, vielleicht aber auch nicht; und wenn sie es nicht tun, dann werden sie dafür sorgen, dass die eine Korrelation, die sie gefunden haben, um einiges beeindruckender wirken wird, als sie ist.
Wenn Korrelationen also fraglich, aber nicht nutzlos sind, wie sollten wir mit ihnen umgehen?
Korrelationen zu finden ist eine nützliche Methode, um Hypothesen zu erstellen, aber es ist eine sehr schwache Methode, um sie zu überprüfen. Mit anderen Worten, wenn eine anscheinende Korrelation gefunden wird, sollte man sie als Hypothese betrachten und nicht als Schlussfolgerung.
Bevor wir zu viele Spekulationen über die Ursache anstellen, ist es besser, zuerst die Korrelation zu untermauern. Eine Möglichkeit besteht darin, in einer neuen Datenmenge nach genau dieser Korrelation zu suchen. Die ursprüngliche Beobachtung der Korrelation ergab sich wahrscheinlich aus vielen beobachteten Korrelationen, viele mehr, als man leichtgläubig für echt halten wird. Man kann dieses versteckte vielfache Vergleichen in den Griff bekommen, indem man ausschließlich nach der einen anscheinenden Korrelation sucht.
Es ist jedenfalls von entscheidender Bedeutung, dass ein neuer und unabhängiger Datensatz verwendet wird. Wenn man die alten Daten dazu nimmt, begünstigt man vielleicht die zufällige Korrelation.
Sobald die Korrelation als wahrscheinlich wahr bestätigt wurde, besteht der nächste Schritt darin, mögliche Kausalbeziehungen zu sondieren. Wenn A mit B korreliert, dann ist es für gewöhnlich möglich, dass A B verursacht, oder dass B A verursacht, oder dass beide mit einem dritten Faktor C in Verbindung stehen. Diese Analyse sollte von einer vorausgehenden Untersuchung der Plausibilität gelenkt werden.
Es korrelieren zum Beispiel viele Dinge mit der Bevölkerungszahl. Also gibt es in jeder Gegend mit wachsender Bevölkerung Korrelationen mit jenen Faktoren, die üblicherweise in Verbindung damit stehen.
Es gibt im Wesentlichen zwei Arten, wie eine spezifische kausale Beziehung bestätigt werden kann – durch Beobachtung und durch Experimente. Der verlässlichste Typ von Daten sind experimentelle Daten, da Störvariablen kontrolliert werden können. Man kann sehen, ob eine Steigerung von A eine Steigerung von B bewirkt oder umgekehrt.
Es ist jedoch nicht immer möglich, kontrollierte Experimente durchzuführen. In diesen Fällen sind weitergehende Daten aus Beobachtung hilfreich. Jede mögliche ursächliche Verknüpfung macht etwa unterschiedliche Vorhersagen, die wiederum verwendet werden können, um die verschiedenen Kausalhypothesen zu überprüfen.
Daten, die durch Beobachtung gewonnen wurden, sind immer fehlerverdächtig, da es eine unbekannte Variable geben kann, um die die Daten nicht bereinigt wurden. Es gibt zum Beispiel Forschungen, die eine Korrelation zwischen Gewalt in Computerspielen und Aggression zeigen. Eine unlängst erschienene Studie jedoch zeigt, dass die Aggression tatsächlich aber mit der Frustration, die ein schwieriges Spiel auslöst, korreliert, und nicht mit dem Grad der Gewalt. (Ich sage nicht, dass damit das letzte Wort gesprochen ist, sondern nur, dass neue Forschungsergebnisse einen anderen beteiligten Faktor aufgedeckt haben, der in früheren Studien nicht berücksichtigt wurde.)
Fazit:
Korrelationen sind ein wichtiger Teil der wissenschaftlichen Forschung. Wir verwenden im täglichen Leben scheinbare Korrelationen, um Schlussfolgerungen zu Ursache und Wirkung ziehen zu können.
Es ist sehr hilfreich, ein nuanciertes Verständnis der komplexen Beziehung zwischen Korrelation und Kausalität zu haben, und für jeden Forscher und auch sonst jeden, der veröffentlichte Forschungsarbeiten verstehen will, ist dies essentiell. Die “Spurious correlations” Website verdeutlicht etwas, das oft die erste Lektion ist, die wir verinnerlichen müssen: Korrelation bedeutet nicht unbedingt Kausalität.
Eben so wenig dürfen wir jedoch Korrelationen von der Hand weisen, denn manchmal sind sie echt und weisen uns auf Kausalität hin. Weitere umsichtige Forschung ist jedoch notwendig, um die Wahrheit einer anscheinenden Korrelation zu bestätigen und dann die wahren Auswirkungen echter Korrelationen zu erforschen.
Übersetzung von: Daniela Bartl, Robert Keller, Übernahme von de.richarddawkins.net