BERLIN. (hpd) Warren Buffet, Unternehmer, Investor und einer der reichsten Menschen auf dem Planeten, schreibt über Derivate: "Wir sehen sie als Zeitbomben, sowohl für die Parteien, die mit ihnen handeln, als auch für das Wirtschaftssystem (…) Grundsätzlich wechselt mit diesen Instrumenten Geld an einem zukünftigen Datum den Besitzer, wobei die Summe von einem oder mehreren Referenzwerten, etwa Zinssätzen, Aktienkursen oder Währungskursen, bestimmt wird." ^[1] Haben das jetzt alle verstanden? Dann der Versuch einer Annäherung:

Das Wort Derivat taucht in verschiedenen Zusammenhängen auf. Man kennt es in der Linguistik, in der Mathematik und in der Chemie. In der Chemie bezeichnet man damit Stoffe, die eine ähnliche Struktur wie eine Grundsubstanz haben und in diesem Sinne von ihr abgeleitet sind. Dabei bezieht man sich auf die Bedeutung des lateinischen Wortes "derivare", was "ableiten" bedeutet. Allerdings wird es auch im Sinne von "abwälzen" verwendet, was der Bedeutung in der Finanzwirtschaft schon näher kommt.

Angenommen, ein Bauer möchte Getreide verkaufen und ein Lebensmittelproduzent möchte es kaufen. Dann können beide Parteien warten, bis das Getreide eingefahren ist, sich auf einen Preis einigen und dann die Sache abwickeln. Aber beide Seiten wollen Planungssicherheit. Deshalb sind sie daran interessiert, möglichst früh Gewissheit über den Preis zu haben. Nun können sie bedenken, was Einfluss auf den Preis des künftigen Getreides haben könnte. Wenn sie darüber Einigkeit erzielen, machen sie einen Vertrag, wonach der Verkäufer zu einem gewissen Preis zusichert, eine bestimmte Menge Getreide zu einem festgesetzten Zeitpunkt zu einem bestimmten Preis an den Käufer zu verkaufen. Danach kümmert sich jeder wieder um seinen Kram und das vielleicht noch nicht einmal gesäte Getreide hat noch etwas Zeit.

Warum ist nun ein solches Geschäft ein Derivat, also ein "Abkömmling" und Abkömmling wovon? Beide Seiten versuchen, ihre Risiken zu verringern. Das Risiko für den Käufer besteht darin, dass der künftige Preis deutlich über dem Durchschnitt liegen kann; etwa dann, wenn weniger verfügbar ist als gedacht. Umgekehrt hat der Bauer Sorge, seine Ware nicht kostendeckend an den Mann zu bringen falls seine Ernte und die seiner Konkurrenz besonders üppig ausfallen und dadurch recht viel angeboten wird. Die Vertragspartner leiten also von Fakten, Erfahrungen und Annahmen ab, welcher Preis angemessen ist und wie hoch sie das Risiko einschätzen, dass es anders kommt als gedacht. Der Preis des Derivats (hier: der Zusicherung von Preis und Menge zu einem bestimmten Zeitpunkt) ist in gewisser Weise die Absicherung gegen dieses Risiko. Insofern ist der Preis für den zugesicherten Handel ein Abkömmling anderer Preise, Risiken, Ernten und Marktentwicklungen. Bis hier scheinen die Wünsche und das Vorgehen der beiden Parteien durchaus nachvollziehbar. Es handelt sich auch nicht um Fiktionen. Es ist vielfach so gemacht worden.^[2] Es sieht auch nichts davon nach "Zeitbombe" aus, wie Buffett schreibt.

Eine Wendung erfährt die Sache, wenn der Käufer des Kaufrechts gar nicht vorhat, dieses jemals einzulösen. Wenn er statt dessen vorhat, sein Kaufrecht bei einer Veränderung der Marktsituation gewinnbringend zu verkaufen, entfernt sich der Vorgang immer mehr vom eigentlichen Produkt. Umgekehrt kann es sein, dass der Verkäufer des Derivats gar nicht im Besitz der betreffenden Ware ist oder es jemals sein wird. Dann wird aus einer nachvollziehbaren Risikoabsicherung ("abwälzen") leicht ein Konzept, das mit realen Waren und deren Werten wenig bis nichts zu tun hat. Selbstverständlich ist die Idee des Derivats leicht auszubauen zu verschiedenen Vertragstypen mit unterschiedlichen Beteiligten, Inhalten, Verpflichtungen und Laufzeiten. So ist es auch geschehen. Derivate können auch selbst Basis von Derivaten werden.

Dafür benötigte man allerdings eine Grundlage. Der Dreh- und Angelpunkt ist die Berechnung der Preise der Derivate und der damit verbundenen Größen (u.a. Preisänderungen bei Änderung der Basiswerte). Hier findet ein Modell Anwendung, dass nach seinen Entwicklern Black-Scholes-Modell genannt wird. Black und Scholes entwickelten es Anfang der 1970er. Eine Grundlage war die Annahme, das Marktgeschehen ließe sich ähnlich beschreiben wie gewisse Vorgänge bei der Wärmeausbreitung bzw. der Brownschen Bewegung. Diese sind in der Physik geläufig und sorgfältig untersucht

Für Genießer: die Black-Scholes-Gleichung:

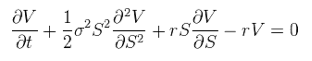
Wenn sich etwas reimt, es dadurch meistens richtig scheint. (Volksmund?)

Umso mehr, wenn es so eine schnuckelige Gleichung ist. Leute, die mit solchen Sachen hantieren, wissen doch, was sie tun. Tun sie doch, oder? Auch wenn manche sich vielleicht nur undeutlich an ihre letzte Auseinandersetzung mit einer Differentialgleichung erinnern, muss das nicht bedeuten, dass man sie kritiklos durchgehen läßt. Denn wichtiger als manche mathematischen Details ist vielleicht, dass es sich um ein Modell handelt, was naturgemäß gewissen Beschränkungen unterliegt. Dieses hier birgt besondere Probleme. Man mag durchaus fragen, ob sich die Vorstellungen über die Wärmeausbreitung besonders gut zur Beschreibung der hier behandelten Vorgänge eignen. Es ist sicher auch eine Diskussion wert, was mit jenen Faktoren ist, die nicht im Modell abgebildet sind, aber das Marktgeschehen gleichwohl beeinflussen.

Was geschieht aber, wenn ein Modell durch massenhafte Anwendung auf sich selbst zurückwirkt und die Dinge beeinflusst, die Grundlage dessen sind, was mit seiner Hilfe berechnet werden soll? Dann wird es zuweilen heikel. Oder mit den Worten von Harald Mumm: "Rückgekoppelte Systeme sind immer gefährlich."

Viele Beteiligte machen in unzähligen Wiederholungen miteinander Geschäfte. Das geschieht oft nach demselben, idealisierten Modell. So können sich auch die Fehler, die Unterschiede zwischen Modell und Realität, irgendwo ansammeln. Jeder versucht, diese von sich fernzuhalten (“abzuwälzen”) und “sichert” seine Geschäfte in endloser Folge nach wieder demselben Modell ab.

Stewart beschreibt das so: "(Derivate) ... sind Anlagen in Anlagen, Versprechungen auf Versprechungen. Die Händler hantieren mit virtuellem Geld, Zahlen im Computer. Sie leihen es sich von Investoren, die es wahrscheinlich selbst woanders geliehen haben. Häufig haben sie es überhaupt nicht geliehen, nicht einmal virtuell; sie sind mit einem Mausklick die Verpflichtung eingegangen, es zu leihen, falls es jemals notwendig sein sollte. Aber sie haben gar nicht die Absicht, es notwendig werden zu lassen; bevor das geschieht, wollen sie das Derivat verkaufen. … Das ist Finanzwesen im Wolkenkuckucksheim…"

Abgesehen davon gibt es auch einen ganz alltäglichen Punkt, der zum Kippen der Sache führen kann: Forderungen sind keine Guthaben. Wenn jemand Forderungen gegen einen anderen hat, also Geld zu bekommen hat, kann er seinerseits auf dieser Grundlage Geld leihen. Forderungen als "Sicherheiten" - das ist kein von vornherein unseriöses Konzept. Es ist durchaus möglich, dass so etwas solide gemacht wird. Aber oft ist es das eben nicht.

Forderungen sind keine Guthaben - ein Beispiel

Leute bekommen bei einer Bank günstig Kredite für Eigenheime. Das spricht sich rum. Die Nachfrage nach Eigenheimen steigt. Dadurch steigen deren Preise. Also gewähren auch andere Banken günstige Kredite für Eigenheime. Das spricht sich weiter herum. Die Eigenheimpreise steigen. Die Banken verkaufen Kredite und machen sich keine Sorgen, denn die Eigenheimpreise steigen. Die Häuser dienen als Sicherheit. Was soll schiefgehen? Schon werden Kredite an Leute verkauft, die sie sich eigentlich nicht leisten können. Das geht einige Zeit gut. Irgendwann können ein paar Leute zuviel ihre Kredite nicht mehr bedienen. Sie verlieren ihre Häuser. Die Banken verkaufen sie. Die Eigenheimpreise sinken. Das spricht sich herum - insbesondere bei den anderen Banken, denen die Eigenheime als Sicherheiten dienen… Die Abwärtsbewegung kann rasend schnell gehen. Die Banken werden die Häuser nicht mehr los, trauen einander nicht mehr, weil sie wissen, die anderen haben auch mit Zitronen gehandelt und gehen unter (oder werden mit Steuermitteln künstlich beatmet).

Es bedarf keiner besonderen Phantasie, um sich vorzustellen, dass solche Prozesse in der Welt computergesteuerter Geschäfte bei weitem schneller ablaufen und mit Derivaten ungleich größere Summen zu erzeugen sind als mit Häusern und Verträgen auf Papier. Umso heftiger ist dann der Absturz, wenn irgendwo einer zu viel nicht zahlen kann und der Trend umkippt. Möglicherweise hatte Warren Buffett bei seiner Bemerkung so etwas im Sinn. Dem könnte man entgegenhalten, dass dies doch wohl nicht so schlimm sein könne, wenn nur mit irgendwelchen Phantasieprodukten hantiert wird. Das mag sein, sofern die Akteure nicht das Bestreben hätten, ihre Phantasieprodukte und Phantasiesummen wenigstens zum Teil gegen "richtige" Waren einzutauschen wie Haus und Auto und Flugticket (oder auch das ganze Flugzeug). Gewöhnlich hält sich dieses Bestreben in gewissen Grenzen, denn wenn das Geld in der Spekulationssphäre bleibt, kann man weiterspielen. In dem Moment aber, in dem Zweifel aufkommen und der Glaube an die Statik des Kartenhauses schwindet, versucht jeder, sein Geld aus der Abenteuersphäre herauszuziehen. Die Blase platzt. Der letzte macht das Licht aus.

Und morgen auf ein Neues….